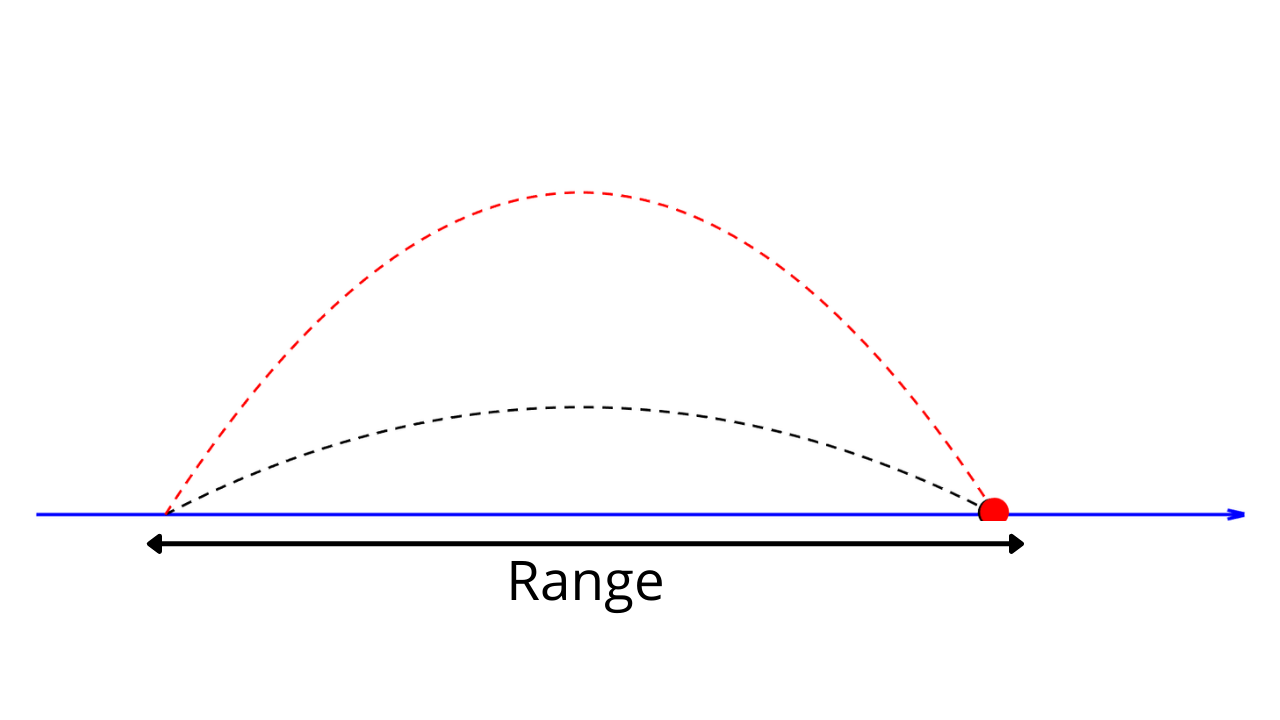
Horizontal Range of Projectile

Horizontal range of a projectile is the horizontal distance travelled by the projectile between launch and the landing points.

We will begin with an expression for the range for a projectile, projected at an angle $\theta$ on a level ground meaning launch and landing points are at the same height. 

Following this we will find out the maximum range of the projectile for a given initial velocity and as we will see it is maximum when angle of projection $\theta = 45^\circ$. 

Afterwards we will see that range is same for $\theta$ and $90^\circ – \theta$. 

In the end we will find out range when ground is not level meaning landing point is at a different height than the launch point, say in case of horizontal projectile motion

So, let’s start with the expression for the range

Range of Projectile, $R$

Horizontal Range of Projectile

Horizontal distance covered by the projectile by the time it returns to the ground is $=u_x \times$ Time of Flight, $T$, where $u_x = u \cos \theta$ is the horizontal component of velocity which does NOT change during the flight as there is no acceleration along the horizontal direction

Time of Flight, $T$, time over which $y$ displacement becomes zero is given by

$0 = u_y T – \cfrac{1}{2} g T^2$ or $T =$ $\cfrac{2 u_y}{g}$ $=\cfrac{2 u \sin \theta}{g}$

which means, Range, $R$ $=\cfrac{2 u^2 \sin \theta \cos \theta}{g}$ $=\cfrac{u^2 \sin 2\theta}{g}$

Maximum Range of Projectile

Now that the range of projectile is given by $R= \cfrac{u^2 \sin 2 \theta}{g}$, when would $R$ be maximum for a given initial velocity $u$. Well, since $g$ is a constant, for a given $u$, $R$ depends on $\sin 2 \theta$ and maximum value of $\sin$ is $1$. So, $R_{max} = \cfrac{u^2}{g}$ and it is the case when $\theta = 45^\circ$ because at $\theta = 45^\circ$, $\sin 2\theta = 1$.

To summarize, for a given $u$, range $R$ is maximum for angle of projection $=45^\circ$.

With that, let’s examine if range $R$ is same for projection angles $\theta$ and $90^\circ – \theta$

Same Range for Two Angles of Projection

Let’s say that range $R$ at projection angle of $\theta_1$ is equal to range at projection angle $\theta_2$, then what is the relation between $\theta_1$ and $\theta_2$

Well this means that $\cfrac{u^2 \sin 2 \theta_1}{g} = $ $\cfrac{u^2 \sin 2 \theta_2}{g}$ or $\sin 2 \theta_1=$ $\sin 2 \theta_2$, which will be true if $2 \theta_2 =$ $180^\circ – 2 \theta_1$ or $\theta_2 = $ $90^\circ – \theta_1$

In other words, for a given velocity a projectile has the same range for $\theta$ and $90^\circ – \theta$.

Range of a projectile launched from a height

Projectile launched from a height at angle $\theta$ with the ground

Assuming that the origin is at the point of launch, let’s say that the time of flight is $T$ (i.e. time it took for the projectile to reach the ground), then

$y$ displacement $=-H=$ $u_y T -$ $\cfrac{1}{2} g T^2$ or $T =$ $\cfrac{u_y + \sqrt{u_y^2+2gH}}{g}$

And horizontal distance covered by projectile during this time, $R$, will be $=u_x T$

Now, let’s see what the expression for $R$ will change to when $u_y=0$, i.e. when projectile is thrown horizontally

 

Horizontal Projectile Motion

Range $= u \times$ Flight Time, $T$

Time of flight is dictated by vertical motion $H = 0.T + \cfrac{1}{2} gT^2$ or $T= \sqrt{\cfrac{2H}{g}}$

Hence, Range = $= u \sqrt{\cfrac{2H}{g}} $

With that, let’s look at trajectory of a projectile.

Projectile Motion | Important Questions | JEE PYQs

    Kinematics Overview – What you need to know for JEE Main and JEE Advanced

      Leave a Reply